Сети с прямыми связями.
1. Простой персептрон. В середине 50-х годов была предложена одна из первых моделей нейронных сетей, которая вызвала большой интерес из-за своей способности обучаться распознаванию простых образов. Эта модель - персептрон - состоит из бинарных нейроподобных элементов и имеет простую топологию, что позволило достаточно полно проанализировать ее работу и создать многочисленные физические реализации.
Типичный персептрон состоит из трех основных компонент:
- матрицы бинарных входов r1..rn
(сенсорных нейронов или «сетчатки», куда подаются входные образы);
- набора бинарных нейроподобных элементов xi… хм (или предикатов в наиболее общем случае) с фиксированными связями к подмножествам сетчатки («детекторы признаков»);
- бинарного нейроподобного элемента с модифицируемыми связями к этим предикатам («решающий элемент»). На самом деле число решающих элементов выбирают равным количеству классов, на которое необходимо разбить предъявляемые персептрону образы.
Таким образом, модель персептрона характеризуется наличием только прямых связей, один из слоев которых является модифицируемым. В простейшем случае, когда п = m и xi == ri, детекторы признаков могут рассматриваться как входной слой. Тогда персептрон становится одним бинарным нейроподобным элементом. Это классическая модель М -входового нейрона, приведенная на рисунке, или простой персептрон Розенблатта. В общем случае каждый элемент xi может рассматриваться как булева функция, зависящая от некоторого фиксированного подмножества сетчатки. Тогда величина выходных сигналов этих обрабатывающих элементов является значением функции xi, которое равно 0 или 1.
Устройство реагирует на входной вектор генерацией выходного сигнала у решающего элемента по формуле (3). Таким образом, персептрон формирует гиперплоскость, которая делит многомерное пространство x1... хм на две части и определяет, в какой из них находится входной образ, выполняя, таким образом, его классификацию. Возникает вопрос, как определить значения весов, чтобы обеспечить решение персептроном конкретной задачи.
Это достигается в процессе обучения.
Предложены различные правила обучения персептрона. Один из алгоритмов называется процедурой сходимости персептрона Розенблатта и является вариантом хеббовского правила изменения весов связей с учителем.
Алгоритм работает следующим образом. Вектор весов

Таким образом, если два класса образов могут быть разделены гиперплоскостью, то при достаточно долгом обучении персептрон будет различать их правильно. Однако линейная разделяющая поверхность, упрощающая анализ персептрона, ограничивает решаемый им круг задач. Этот вопрос тщательно исследовали Минский и Пейперт, показав, какие задачи в принципе не может решить персептрон с одним слоем обучаемых связей. Одним из таких примеров является выполнение логической операции «исключающее ИЛИ».
2. Многослойный персептрон. Как отмечалось выше, простой персептрон с одним слоем обучаемых связей формирует границы областей решений в виде гиперплоскостей. Двухслойный персептрон может выполнять операцию логического «И» над полупространствами, образованными гиперплоскостями первого слоя весов. Это позволяет формировать любые, возможно неограниченные, выпуклые области в пространстве входных сигналов. С помощью трехслойного персептрона, комбинируя логическими «ИЛИ» нужные выпуклые области, можно получить уже области решений произвольной формы и сложности, в том числе невыпуклые и несвязные. То, что многослойные персептроны с достаточным множеством внутренних нейроподобных элементов и соответствующей матрицей связей в принципе способны осуществлять любое отображение вход-выход, отмечали еще Минский и Пейперт, однако они сомневались в том, что можно открыть для них мощный аналог процедуры обучения простого персептрона.
В настоящее время в результате возрождения интереса к многослойным сетям предложено несколько таких процедур. В данном параграфе описана детерминированная версия, получившая название « error back propagation» - алгоритм обратного распространения ошибки. Этот алгоритм является обобщением одной из процедур обучения простого персептрона, известной как правило Уидроу - Хоффа (или дельта-правило), и требует представления обучающей выборки. Выборка состоит из набора пар образов, между которыми надо установить соответствие, и может рассматриваться как обширное задание векторной функции, область определения которой - набор входных образов, а множество значений - набор выходов.
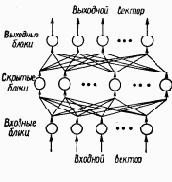
Рассмотрим многослойную нейроподобную сеть с прямыми связями (см. рисунок). Входные элементы (блоки) образуют нижний слой сети, выходные - верхний. Между ними может быть много слоев скрытых блоков. Каждый блок может быть соединен модифицируемой связью с любым блоком соседних слоев, но между блоками одного слоя связей нет. Каждый блок может посылать выходной сигнал только р вышележащие слои и принимать входные сигналы только от нижележащих слоев. Входной вектор подается на нижний слой, а выходной вектор определяется путем поочередного вычисления уровней активности элементов каждого слоя (снизу - вверх) с использованием уже известных значений активности элементов предшествующих слоев. С точки зрения распознавания образов входной вектор соответствует набору признаков, а выходной - классу образов. Скрытый слой используется для представления области знаний.
Перед началом обучения связям присваиваются небольшие случайные значения. Каждая итерация процедуры состоит из двух фаз. Во время первой фазы на сеть подается входной вектор путем установки в нужное состояние входных элементов. Затем входные сигналы распространяются по сети, порождая некоторый выходной вектор. Для работы алгоритма требуется, чтобы характеристика вход-выход нейроподобных элементов была неубывающей и имела ограниченную производную. Обычно для этого используют сигмоидную нелинейность вида (4).
Полученный выходной вектор сравнивается с требуемым. Если они совпадают, обучение не происходит. В противном случае вычисляется разница между фактическими и требуемыми выходными значениями, которая передается последовательно от выходного слоя к входному. На основании этой информации об ошибке производится модификация связей в соответствии с обобщенным дельта правилом, которое имеет вид:

где изменение в силе связи wij для р-й обучающей пары пропорционально произведению сигнала ошибки д j-го блока, получающего входной сигнал по этой связи, и выходного сигнала блока i, посылающего сигнал по этой связи. Определение сигнала ошибки является рекурсивным процессом, который начинается с выходных блоков. Для выходного блока сигнал ошибки:

где djp и ojp - желаемое и действительное значения выходного сигнала j-го блока; уj' - производная нелинейности блока. Сигнал ошибки для скрытого блока определяется рекурсивно через сигнал ошибки блоков, с которым соединен его выход, и веса этих связей:

Для используемой сигмоидной нелинейности уj| = уj (1 - уj), поэтому для 0Ј уjЈ1 производная максимальна при уj == 0,5 и равна нулю при уj =0 или 1. Соответственно веса изменяются максимально для блоков, которые еще не выбрали свое состояние. Кроме того, при конечных весах выходные сигналы блоков не могут достигать значений 0 или 1, Поэтому за 0 обычно принимают значения уj < 0.1, а за 1 - значения уj > 0.9.
Модификация весов производится после предъявления каждой пары вход - выход. Однако если коэффициент h, определяющий скорость обучения, мал, то можно показать, что обобщенное дельта-правило достаточно хорошо аппроксимирует минимизацию общей ошибки функционирования сети D методом градиентного спуска в пространстве весов. Общая ошибка функционирования сети определяется так:

Обучение продолжается до тех пор, пока ошибка не уменьшится до заданной величины. Эмпирические результаты свидетельствуют о том, что при малых h система находит достаточно хороший минимум D.
Один из основных недостатков алгоритма обратного распространения, однако, заключается в том, что во многих случаях для сходимости может потребоваться многократное (сотни раз) предъявление всей обучающей выборки.
Повышения скорости обучения добиваются, например, использованием информации о второй производной D, увеличением h. В последнем случае избежать осцилляций позволяет инерционный член:

где a - экспоненциально затухающий множитель, определяющий относительное воздействие текущего и прошлых градиентов на изменение веса.
Предпринимаются попытки использовать алгоритм обратного распространения ошибки для обучения сетей с обратными связями обработки последовательностей образов. Основой для этого является эквивалентность многослойной сети с прямыми связями и синхронной сети с обратными связями на ограниченном временном интервале (слой соответствует такту времени). Предложены также варианты алгоритмов обучения, более привлекательные с биологической точки зрения. Таким, например, является алгоритм рециркуляции, предложенный для сетей, в которых скрытые блоки соединены со входными. При обучении веса связей перестраиваются таким образом, чтобы минимизировать частоту смены активности каждого блока. Таким образом, обученная сеть имеет стабильные состояния и может функционировать в режиме ассоциативной памяти.
В настоящее время многослойные персептроны являются наиболее популярной моделью нейронных сетей. Это в значительной степени объясняется тем, что с их помощью удалось продемонстрировать решение ряда задач, в том числе классической для персептронов задачи «исключающего ИЛИ», задачи синтеза речи по тексту, а также задач, требующих принятия экспертных решений. Возможно, что подобные многослойным персептронам нейронные структуры используются мозгом для предварительной обработки сенсорной информации, например, при выделении признаков.